Orthogonal Frequency Division Multiplexing (OFDM)

The contents of this article are taken from different sources.

 OFDM

Introduction

Digital multimedia applications as they are getting common lately create an ever increasing demand for broad band communication systems. Although the technical requirements for related products are very high the solutions must be cheap to implement since we are basically talking about consumer products.

Whereas for the satellite channel and for the cable channel such cost-efficient solutions already exist for the terrestrial link (i.e. classical TV broadcasting) the requirements are so high that the 'standard' solutions are no longer feasible or lead to sub optimal results. Orthogonal Frequency Division Multiplexing (OFDM) is a method that allows to transmit high data rates over extremely hostile channels at a comparable low complexity. OFDM has been chosen as the transmission method for the European radio (DAB) and TV (DVB-T) standard. Due to its numerous advantages it is under Discussion for future broadband application such as wireless ATM as well.

OFDM and the orthogonality principle

The general problem: Data transmission over multipath channels

Differently from satellite communication where we have one single direct path from transmitter to receiver in the classical terrestrial broadcasting scenario we have to deal with a multipath- channel: The transmitted signal arrives at the receiver in various paths (see figure 1) of different length. Since multiple versions of the signal interfere with each other (inter symbol interference (ISI)) it becomes very hard to extract the original information.

  
Figure 1: Multipath transmission in a broadcasting application

The common representation of the multipath channel is the channel impulse response (cir) of the channel which is the signal at the receiver if a single pulse is transmitted (figure 2).

  
Figure 2: Effective length of cir

Let's assume a system transmitting discrete information in time intervals T. The critical measure concerning the multipath-channel is the delay of the longest path with respect to the earliest path. A received symbol can theoretically be influenced by previous symbols. This influence has to be estimated and compensated for in the receiver, a task which may become very challenging.

Single carrier approach

In figure 3 the general structure of a single carrier transmission system is depicted. The transmitted symbols are pulse formed by a transmitter filter. After passing the multipath channel in the receiver a filter matched to the channel is used to maximize signal to noise ratio a device used to extract the data.

  
Figure 3: Basic structure of a single carrier system

The scenario we are dealing with in DVB-T is characterized by the following conditions:

           Transmission Rate:

           Maximum channel delay:

For the single carrier system this results in an ISI of: 

The complexity involved in removing this interference in the receiver is tremendous. In the scenario under consideration here, using such an approach will only lead to sub-optimal results. This is the main reason why the multi carrier approach is used.

Multi carrier approach

Figure 4 shows the general structure of a multicarrier system. 

  
Figure 4: Basic structure of a multicarrier system

The original data stream of rate R is multiplexed into N parallel data streams of rate 

each of the data streams is modulated with a different frequency and the resulting signals are transmitted together in the same band. Correspondingly the receiver consists of N parallel receiver paths. Due to the prolonged distance in between transmitted symbols the ISI for each sub system reduces to 

In the case of DVB-T we have N=8192 leading to an ISI of 

Such little ISI can often be tolerated and no extra counter measure such as an equalizer is needed. Alas as far as the complexity of a receiver is concerned a system with 8192 parallel paths still isn't feasible. This asks for a slight modification of the approach which leads us to the concept of OFDM.

Orthogonal Frequency Division Multiplexing

In OFDM the subcarrier pulse used for transmission is chosen to be rectangular. This has the advantage that the task of pulse forming and modulation can be performed by a simple Inverse Discrete Fourier Transform (IDFT) which can be implemented very efficiently as a I Fast Fourier Transform (IFFT). Accordingly in the receiver we only need a FFT to reverse this operation. According to the theorems of the Fourier Transform the rectangular pulse shape will lead to a sin(x)/x type of spectrum of the subcarriers (see figure 5).

  
Figure 5: OFDM and the orthogonality principle

Obviously the spectrums of the subcarriers are not separated but overlap. The reason why the information transmitted over the carriers can still be separated is the so called orthogonality relation giving the method its name. By using an IFFT for modulation we implicitly chose the spacing of the subcarriers in such a way that at the frequency where we evaluate the received signal (indicated as arrows) all other signals are zero. In order for this orthogonality to be preserved the following must be true:

1. The receiver and the transmitter must be perfectly synchronized. This means they both must assume exactly the same modulation frequency and the same time-scale for transmission (which usually is not the case).
2. The analog components, part of transmitter and receiver, must be of very high quality.
3. There should be no multipath channel.

In particular the last point is quite a pity, since we have chosen this approach to combat the multipath channel. Fortunately there's an easy solution for this problem: The OFDM symbols are artificially prolonged by periodically repeating the 'tail' of the symbol and precede the symbol with it (see figure 5). At the receiver this so called guard interval is removed again. As long as the length of this interval is longer than the maximum channel delay all reflections of previous symbols are removed and the orthogonality is preserved. Of course this is not for free, since by preceding the useful part of length by the guard interval we lose some parts of the signal that cannot be used for transmitting information. Taking all this into account the signal model for the OFDM transmission over a multipath channel becomes very simple: The transmitted symbols at time-slot l and subcarrier k are only disturbed by a factor which is the channel transfer function (the fourier transform of the cir) at the subcarrier frequency, an by additional white Gaussian noise n

 

 

The influence of the channel can easily be removed dividing by.

As far as the analog components are concerned experience has shown that in the broadcasting applications under consideration here, they are not so critical. What remains is to establish 'perfect' synchronization. This requires a very sophisticated receiver. The general structure and the receiver of such a receiver which we have developed for the DVB-T application.

An OFDM receiver for DVB-T

Tasks of the inner receiver and receiver structure

As mentioned before in order for a digital transmission system to work, receiver and transmitter have to be synchronized. This involves the following tasks:

• Timing synchronization: Since it is unknown to the receiver, to which exact (absolute) time instant the symbol has been transmitted and how long the dispersion of the channel is, one essential task is to find the 'beginning' of a received OFDM symbol. Thus the time scales of transmitter and receiver are synchronized and the removal of the guard interval can be done with the required accuracy.
• Frequency synchronization: The signal is usually not transmitted in baseband but modulated with a radio carrier at a frequency assigned by the standard. Though this frequency is known to the receiver the tolerance of the RF components usually applied is so large that there will be a frequency-deviation. In many cases this deviation will be too large for a reliable data transmission. It therefore must be estimated and compensated at the receiver.
• Sampling-clock synchronization: The signal produced by the FFT will be converted into an analog signal assuming a certain span of time between two values. At the receiver the down converted RF signal is sampled in order to obtain a discrete time signal for further (digital) processing. The sampling times assumed in the receiver must match very accurately in order to avoid a degradation of the performance. A possible deviation between transmitter and receiver must again be estimated and compensated.
• Channel estimation: If a coherent modulation scheme is used (which must not be necessarily the case) according to equation (0.4) the channel transfer function must be estimated and compensated.

A receiver structure that allows to estimate and compensate all parameters required is depicted in figure 6. 

  
Figure 6: Receiver structure for a DVB-T receiver

In addition to the elementary tasks found in single carrier receivers too for the receiver under consideration here two further tasks can be identified:

1. TPS detection: So called TPS (transmission parameter signaling) data is provided in DVB-T to inform the receiver about the modulation and coding scheme used. This information is provided via selected subcarriers that are modulated in a robust differential BPSK.
2. CPE detection (and correction): The common phase error (CPE) is a phenomena that results from imperfections of the oscillators used for modulation and demodulation. Instead of providing a stable frequency real oscillators tend to provide a frequency that is slowly changing in time. This change in time leads to an additional modulation of the OFDM signal which in some cases must be estimated and compensated. For the constellations used in DVB-T it can be shown that due to other reasons the quality of the oscillators must be so high that this effect can be neglected.

We will not go into detail as far as the implementation of the single components. What proves to be the most critical component of the receiver is the channel estimation unit. We will therefore go a little more into detail.

Channel estimation for OFDM

The method of channel estimation implied by the frame structure of DVB-T is channel estimation via interpolation. The basic principle is depicted in figure 7. 

  
Figure 7: Principle of channel estimation via interpolation

Embedded into the OFDM data stream are training symbols (depicted as arrows) that can be used to obtain samples of the channel transfer function.

 

The values of the channel in between the samples can then be obtained via a interpolation procedure. Generally we have a two dimensional interpolation problem. Fortunately the problem can be separated into a interpolation in time and in frequency. The most critical task is the design of the interpolation filters used. Both interpolations must agree with the sampling theorem:

• The interpolation in time is bandlimited by the time-variant behavior of the channel. This is cause by a movement of the receiver and by uncompensated synchronization errors. The maximum allowable bandwidth of these disturbances is determined by the number of training symbols in one subcarrier.
• Due to the duality of time and frequency the interpolation in frequency is bandlimited by the length of the cir. The maximum allowable cir-length thus is not only determined by the length of the guard interval but also by the number of training symbols in one OFDM symbol. If we use fixed filters for implementation where the maximum dispersion to be assumed is given by the length of the guard interval this implies that for short guard intervals the channel can be estimated with a higher accuracy than with a larger guard interval.

For interpolation in frequency a interpolation filter optimized according to the Wiener filter theory is used. For interpolation in time a linear interpolation is sufficient.

 Performance of the complete receiver

Figure 8 shows the results achievable with the channel-estimator described in the previous section. The application is a DVB-T receiver according to the European standard operating in 8k mode.

  
figure 8: Achievable performance for different channel estimators

As we can see the achievable system performance very much depends on the achievable quality of the channel estimator. Since it is higher for small cirs thus the performance of the receiver will be better. The loss with respect to the performance with ideal channel estimation ranges from about 0.5 dB for the smallest guard interval up to 1.6 dB for the largest guard interval. Also included are the results for a dynamic channel. Using linear interpolation in time will not further degrade the system. Alas if we try do without any interpolation in time the additional loss in performance is significant.

Key Terms and Details for Refference

DAB

Digital Audio Broadcasting (DAB) is a digital radio technology for broadcasting radio stations, used in several countries, particularly in Europe. As of 2006, approximately 1,000 stations worldwide broadcast in the DAB format.

The DAB standard was initiated as a European research project in the 1980s, and the BBC launched the first DAB digital radio in 1995. DAB receivers have been available in many countries since the end of the nineties. DAB may offer more radio programmes over a specific spectrum than analogue FM radio. DAB is more robust with regard to noise and multipath fading for mobile listening, since DAB reception quality first degrades rapidly when the signal strength falls below a critical threshold, whereas FM reception quality degrades slowly with the decreasing signal.

An "informal listening test" by Professor Sverre Holm has shown that for stationary listening the audio quality on DAB is lower than FM stereo, due to most stations using a bit rate of 128 kbit/s or less, with the MP2 audio codec, which requires 160 kbit/s to achieve perceived FM quality. 128 kbit/s gives better dynamic range or signal-to-noise ratio than FM radio, but a more smeared stereo image, and an upper cutoff frequency of 14 kHz, corresponding to 15 kHz of FM radio. However, "CD sound quality" with MP2 is possible "with 256..192 kbps".

DAB+

An upgraded version of the system was released in February 2007, which is called DAB+. DAB is not forward compatible with DAB+, which means that DAB-only receivers will not be able to receive DAB+ broadcasts. DAB+ is approximately twice as efficient as DAB due to the adoption of the AAC+ audio codec, and DAB+ can provide high quality audio with as low as 64kbit/s. Reception quality will also be more robust on DAB+ than on DAB due to the addition of Reed-Solomon error correction coding.

More than 20 countries provide DAB transmissions, and several countries, such as Australia, Italy, Malta and Switzerland, have started transmitting DAB+ stations. See Countries using DAB/DMB. However, DAB radio has still not replaced the old FM system in popularity.

DVB-T

DVB-T is an abbreviation for Digital Video Broadcasting — Terrestrial; it is the DVB European-based consortium standard for the broadcast transmission of digital terrestrial television that was first publicated in 1997 and first broadcast in the UK in 1998. This system transmits compressed digital audio, video and other data in an MPEG transport stream, using coded orthogonal frequency-division multiplexing (COFDM or OFDM) modulation.

FFT

A fast Fourier transform (FFT) is an efficient algorithm to compute the discrete Fourier transform (DFT) and its inverse. There are many distinct FFT algorithms involving a wide range of mathematics, from simple complex-number arithmetic to group theory and number theory; this article gives an overview of the available techniques and some of their general properties, while the specific algorithms are described in subsidiary articles linked below.

A DFT decomposes a sequence of values into components of different frequencies. This operation is useful in many fields (see discrete Fourier transform for properties and applications of the transform) but computing it directly from the definition is often too slow to be practical. An FFT is a way to compute the same result more quickly: computing a DFT of N points in the naive way, using the definition, takes O(N2) arithmetical operations, while an FFT can compute the same result in only O(N log N) operations. The difference in speed can be substantial, especially for long data sets where N may be in the thousands or millions—in practice, the computation time can be reduced by several orders of magnitude in such cases, and the improvement is roughly proportional to N / log(N). This huge improvement made many DFT-based algorithms practical; FFTs are of great importance to a wide variety of applications, from digital signal processing and solving partial differential equations to algorithms for quick multiplication of large integers.

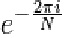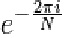The most well known FFT algorithms depend upon the factorization of N, but (contrary to popular misconception) there are FFTs with O(N log N) complexity for all N, even for prime N. Many FFT algorithms only depend on the fact that is an Nth primitive root of unity, and thus can be applied to analogous transforms over any finite field, such as number-theoretic transforms.

Since the inverse DFT is the same as the DFT, but with the opposite sign in the exponent and a 1/N factor, any FFT algorithm can easily be adapted for it.

DFT

The discrete Fourier transform (DFT) is a specific kind of Fourier transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function (which is often a function in the time domain). But the DFT requires an input function that is discrete and whose non-zero values have a limited (finite) duration. Such inputs are often created by sampling a continuous function, like a person's voice. Unlike the discrete-time Fourier transform (DTFT), it only evaluates enough frequency components to reconstruct the finite segment that was analyzed. Using the DFT implies that the finite segment that is analyzed is one period of an infinitely extended periodic signal; if this is not actually true, a window function has to be used to reduce the artifacts in the spectrum. For the same reason, the inverse DFT cannot reproduce the entire time domain, unless the input happens to be periodic (forever). Therefore it is often said that the DFT is a transform for Fourier analysis of finite-domain discrete-time functions. The sinusoidal basis functions of the decomposition have the same properties.

The input to the DFT is a finite sequence of real or complex numbers (with more abstract generalizations discussed below), making the DFT ideal for processing information stored in computers. In particular, the DFT is widely employed in signal processing and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers. A key enabling factor for these applications is the fact that the DFT can be computed efficiently in practice using a fast Fourier transform (FFT) algorithm.

FFT algorithms are so commonly employed to compute DFTs that the term "FFT" is often used to mean "DFT" in colloquial settings. Formally, there is a clear distinction: "DFT" refers to a mathematical transformation or function, regardless of how it is computed, whereas "FFT" refers to a specific family of algorithms for computing DFTs. The terminology is further blurred by the (now rare) synonym finite Fourier transform for the DFT, which apparently predates the term "fast Fourier transform" (Cooley et al., 1969) but has the same initialism.

ISI (intersymbol interference)

intersymbol interference (ISI) is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable. ISI is usually caused by multipath propagation or the inherent non-linear frequency response of a channel causing successive symbols to "blur" together. The presence of ISI in the system introduces errors in the decision device at the receiver output. Therefore, in the design of the transmitting and receiving filters, the objective is to minimize the effects of ISI, and thereby deliver the digital data to its destination with the smallest error rate possible. Ways to fight intersymbol interference include adaptive equalization and error correcting codes.